No campo da geometria espacial temos diversas figuras sólidas que são parte do nosso cotidiano, hoje destacaremos o prisma. Ele sobressai as outras formas por sua variedade, enquanto conserva características comuns entre esses diversos tipos.
Os pontos elementares para considerar um prisma são:
- ser um poliedro convexo, de forma mais prolixa, se tivermos quaisquer dois pontos pertencentes a superfície desse poliedro, o segmento que tem esses pontos como extremidades está inteiramente contido no poliedro;
- ter faces laterais planas (paralelogramos);
- bases poligonais congruentes (de mesmo tamanho e forma) e paralelas.
Mas antes um pouco de aprofundarmos nessas questões, vamos entender do que se trata a geometria espacial?
Geometria espacial
A Geometria é um campo da Matemática que estuda os diferentes aspectos, tamanhos, formas e dimensões dos objetos que existem no espaço. A palavra geometria vem da junção dos termos em grego geo, que significa terra e metria, que se refere à medida.
Desse modo, podemos inferir que a geometria, de modo geral, estuda três elementos principais: comprimento, área e volume de cada objeto no espaço. Outras características analisadas nos estudos geométricos, que são aspectos das formas geométricas, são: pontos, linhas, superfície e volume.
A partir dessas quatro características, podemos classificar as formas geométricas em: planas (figuras que não possuem volume) e não planas. E a geometria espacial trata especificamente das formas não planas, em outros termos aquelas que possuem todos as quatro características.
Outra forma de considerar a Geometria Espacial é como o campo da matemática que estuda objetos que possuem mais de uma dimensão e ocupam lugar no espaço, também chamados de sólidos geométricos ou figuras geométricas espaciais.
Alguns deles são: cubo, pirâmide, cone, cilindro, esfera, paralelepípedo e, a estrela do nosso texto, o prisma. Se pararmos para observar, essas formas fazem parte do nosso cotidiano, como por exemplo: uma caixa tem formato de cubo, uma casquinha de sorvete expresso tem a forma de um cone, uma caixa de Toblerone tem o formato de um prisma!
O que é prisma
Então, afinal, o que é um prisma?
O prisma é caracterizado por ser um sólido geométrico formado por dois polígonos congruentes (de mesma forma e tamanho) contidos em dois planos paralelos, de modo que cada vértice de um desses polígonos esteja conectado ao vértice correspondente do outro por meio de uma aresta.
Além dos planos (ou faces) paralelas, um prisma é composto de altura, lados, vértices e arestas ligados por paralelogramos. E segundo sua inclinação, esses sólidos geométricos podem ser retos (com ângulo de 90°) ou oblíquos (ângulos diferentes de 90°).
Lembrando que os prismas podem ter formatos sólidos diversos, isso vai depender do formato das suas bases paralelas, que podem ter um formato triangular, quadrangular, pentagonal, hexagonal e assim pode diante.
Composição do prisma
Lembra que a geometria espacial analisa os aspectos das formas geométricas? Então, até aqui sabemos que o prisma é um sólido geométrico que faz parte desse campo da matemática, logo, quais são os aspectos que enquadram o prisma nessa categoria?
Temos que considerar os pontos, linhas, superfícies e o volume desse sólido geométrico, que são referenciados da seguinte maneira:
- Faces do prisma: todos os polígonos que limitam um prisma é uma de suas faces, podemos considerar que existem dois tipos de face, as bases do prisma e as faces laterais;
- Bases do prisma: obrigatoriamente precisam ser do mesmo tamanho e a mesma foram (congruentes), depois de atender a esse critério qualquer polígono, como triângulos, quadrados, pentágonos, quadriláteros, pode servir de base para um prisma;
- Faces laterais: são todos os polígonos que fecham o sólido que não seja uma base. Uma característica constante das faces laterais é que elas são um paralelogramo. Isso acontece porque o plano e o polígono são paralelos, fazendo com que um par de lados opostos dessas faces seja paralelo e quando unidos eles compõem o paralelogramo;
- Arestas: são os segmentos de reta compostos pelo encontro de duas faces de um prisma. Temos dois tipos de arestas, as arestas da base a as laterais;
- Arestas da base: são formadas pelos segmentos de reta compostos pelo encontro de uma das bases com uma das faces laterais;
- Arestas laterais: segmentos de reta compostos pelo encontro de duas faces laterais;
- Vértices: são os pontos de encontro entre duas ou mais arestas;
- Diagonais: são linhas que ligam dois vértices que não pertencem à mesma face do prisma;
- Secção transversal: é a intersecção do prisma com algum plano paralelo às bases.
Para que alguns desses pontos fiquem mais evidentes observe a imagem do prisma abaixo. A partir dela é possível identificar os seguintes elementos:
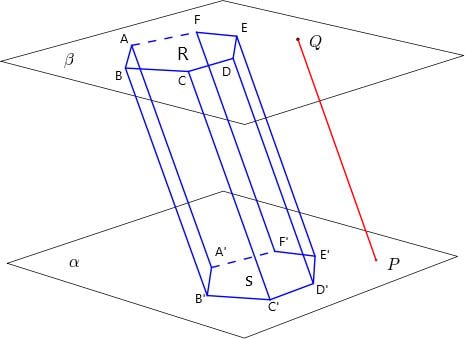
- R e S são as bases das regiões poligonais;
- Altura é a distância h entre os planos a e ß, que podemos considerar como o segmento de reta (QP);
- Os pontos A, B, C, D, E, F e A’, B’, C’, D’, E’, F’ são os vértices do prisma;
- As arestas das bases são os lados (AB), (BC), (CD), (DE), (EF), (FA), (A’ B’), (B’C’), (C’D’), (D’ E’), (E’F’), (F’A’);
- As arestas laterais são os segmentos (AA’), (BB’), (CC’), (DD’), (EE’), (FF’);
- As diagonais são os segmentos de reta (AD’), (BE’), (CF’), (DA’), (EB’), (FC’);
- As faces laterais são os paralelogramos (AA’BB’), (BB’C’C), (CC’D’D), (DD’E’E), (EE’FF’) (FF’A’A);
- As secções transversais são Rβ e Sα
Nomenclaturas do prisma
Tenha em mente que o polígono da base é determinante na formação do sólido geométrico do prisma, então de acordo com o formato das bases, os prismas são nomeados e classificados da seguinte forma:
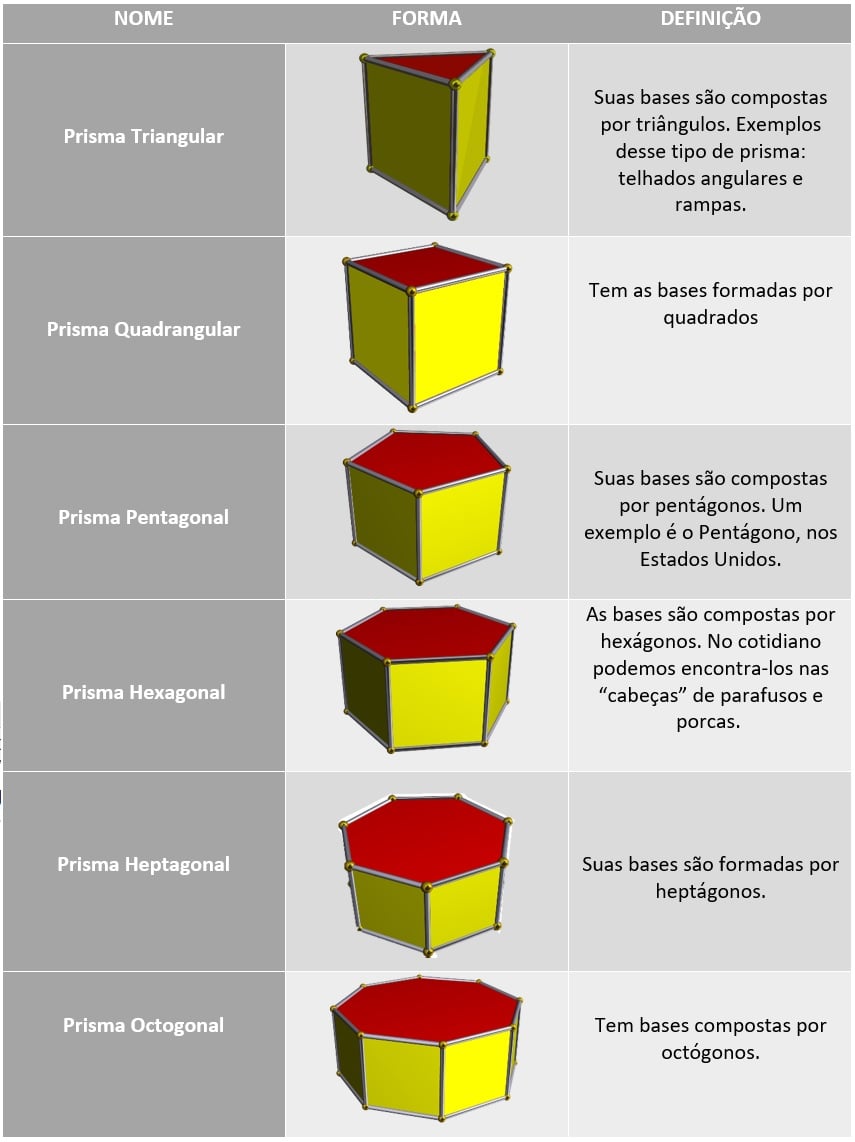
Essa classificação se estende à outras nomenclaturas com base no número de lados do polígono que compõe a base da forma geométrica.
Classificação do prisma
Tanto a inclinação, como o ângulo formado entre as arestas laterais e as bases nos ajudam a classificar e diferenciar os prismas em duas categorias: retos, oblíquos ou regulares.
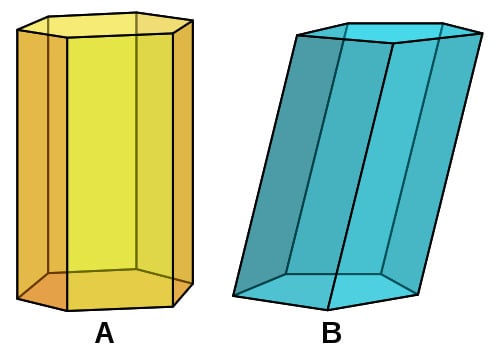
Prisma reto (A)
Quando um prisma que possui arestas laterais perpendiculares (ângulos de 90°) aos planos das bases, ele é chamado de prisma reto. Portanto, a medida da altura dessas figuras é igual a medida das arestas laterais. Repare que as faces laterais de um prisma reto são retângulos.
Prisma oblíquo (B)
Enquanto que, um sólido geométrico com arestas laterais que formam um ângulo diferente de 90° com o plano das bases são chamados de prismas oblíquos. No caso desse tipo de prisma, as faces laterais são compostas de paralelogramos.
Prisma regular
Para classificarmos uma figura geométrica espacial como um prisma regular, ele precisa ter bases que são polígonos regulares, ou seja, somente se todos os lados possuírem a mesma medida e todos os ângulos internos forem congruentes entre si.
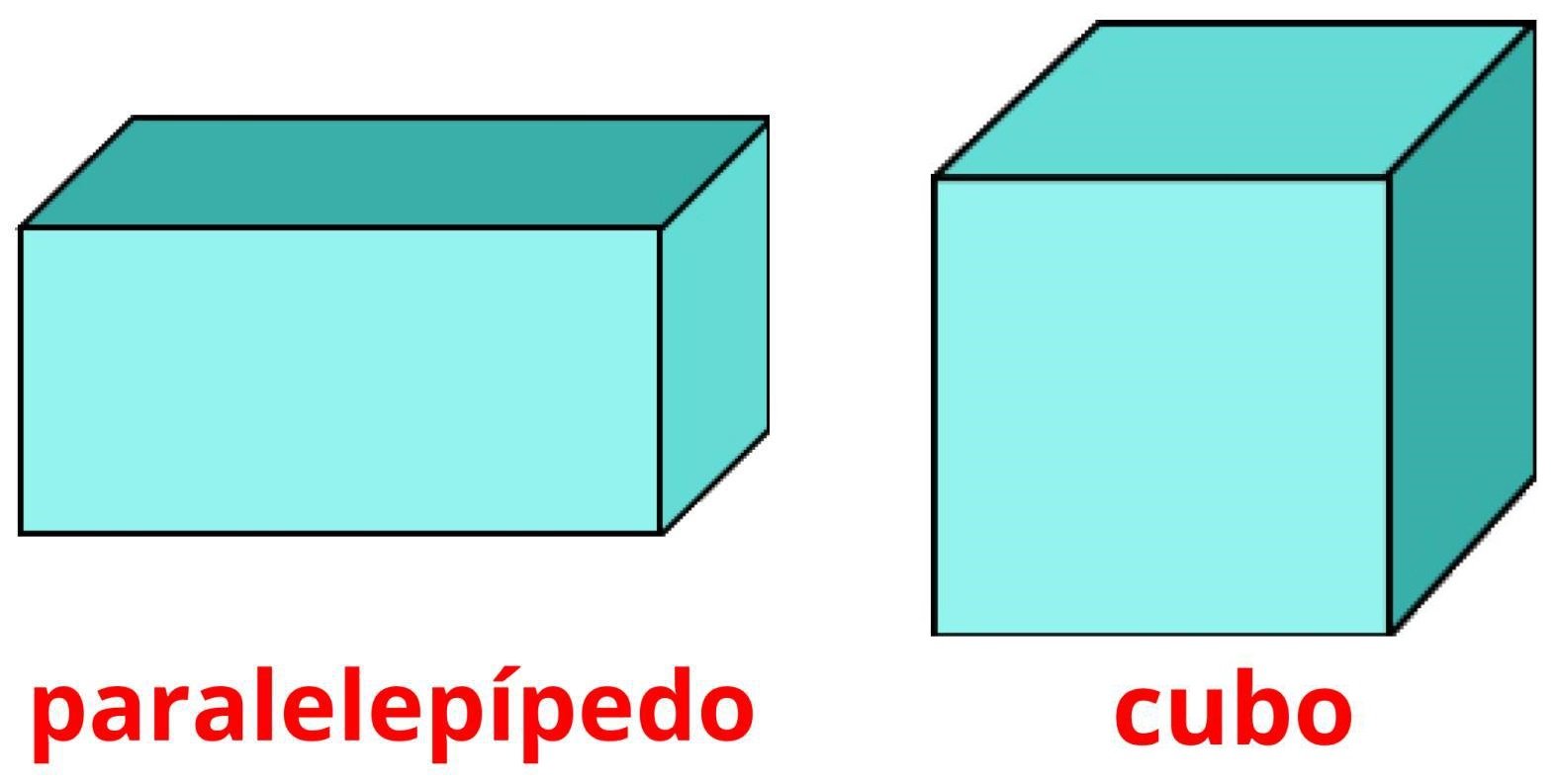
Observe que, se caso tenhamos um prisma com todas as faces quadradas, teremos um cubo. Ao passo que, se todas as faces forem paralelogramos, esse tipo de prisma é conhecido como um paralelepípedo.
Fórmulas do prisma
Até aqui abordamos esse tema de forma totalmente teórica, mas não há matemática sem cálculos, não é mesmo? Então, nos tópicos a seguir vamos apresentar as principais fórmulas para realizar cálculos e descobrir as medidas de um prisma.
Áreas do prisma
Um prisma possui três tipos de áreas calculáveis: a área lateral, a área total e a área da base.
Área lateral
Usamos esse cálculo para encontrar a área que compreende toda superfície do sólido, sem contar suas bases poligonais. Então, para calcular a área lateral de um prisma qualquer usamos a fórmula: , sendo “H” a altura do prisma, “l” o tamanho do lado do polígono da base e “n” o número de vértices do polígono da base.
Caso estejamos trabalhando com um prisma reto, que possui todas as áreas das faces laterais congruentes teremos a seguinte fórmula: , sendo “n” o número de lados e “a” face lateral.
Área Total
A fórmula da área total de um prisma é dada pela adição da área lateral com as áreas das duas bases poligonais, considerando toda superfície do sólido. Em outras palavras, a área total de um sólido é dada por toda região plana que o sólido pode cobrir.
Desse modo, temos a seguinte fórmula para o cálculo da área total de um prisma qualquer: , sendo “” a soma das áreas das faces laterais e “” a soma das áreas das bases.
Área da base
A forma de calcular a área da base de um prisma vai variar de acordo com o formato do polígono que ele apresenta. Por exemplo:
- Prisma triangular regular:
- Prisma quadrangular:
- Prisma hexagonal: para realizar o cálculo desse tipo de base é necessário dividir o hexágono em pequenos triângulos equiláteros, de modo que temos a seguinte fórmula:
Volume do prisma
Quando falamos em volume de um prisma, consideramos a medida espacial do seu interior, em outras palavras, da capacidade do sólido em questão em uma unidade de medida tridimensional.
Para descobrir o volume de um prisma qualquer, precisamos considerar uma base poligonal de determinada área , em seguida podemos sobrepor infinitas (n) bases idênticas sucessivamente até que elas cubram determinado espaço, alinhadas por um segmento de reta “H” que é perpendicular (ângulo de 90°) aos planos que têm bases consecutivas.
Desse modo, é possível sobrepor as duas superfícies da base H vezes, produzindo a fórmula do volume do prisma que será: , em palavras mais simples, o volume do prisma é o resultado do produto entre a área de sua base e sua altura.
Sobre os paralelepípedos
Na matemática alguns prismas aparecem com frequência, assim como o são no dia-a-dia, por conta disso eles ganharam um estudo mais aprofundado de suas formas e definições, chegando possuir nomes exclusivos.
De modo geral, esses prismas são classificados como prismas notáveis, hoje falaremos especificamente do paralelepípedo. De modo bem simples, os paralelepípedos são prismas cujas bases são formadas por paralelogramos.
Além dessa denominação, esses sólidos geométricos também podem ser classificados como oblíquos ou retas. Quando suas bases são retângulos, eles recebem o nome de paralelepípedo reto-retângulo ou bloco retangular,
Fórmulas do paralelepípedo retângulo reto
Como já sabemos, o paralelepípedo retângulo reto é um prisma de base retangular de lados e e uma altura H.
Para calcular a área lateral desse prisma, podemos usar a fórmula , dado que todo retângulo tem quatro lados delimitando, consequentemente, quatro faces para o prisma.
Já o cálculo da área total dessa figura sólida, assim como em qualquer outro prisma, é dado pela soma das áreas da base com a área lateral. Desse modo temos: , ou também podemos usar: .
A fórmula do volume do paralelepípedo é dada por , visto que a área de todo retângulo é dada por .
Além dessas possibilidades de cálculo já citadas, também é possível descobrir a diagonal interna do paralelepípedo.
A diagonal de um sólido é definida por um segmento de reta dado pela ligação de dois vértices não consecutivos, no caso da imagem abaixo belos pontos , que calculamos por meio da fórmula , dado que a diagonal d da face da base é dada por .
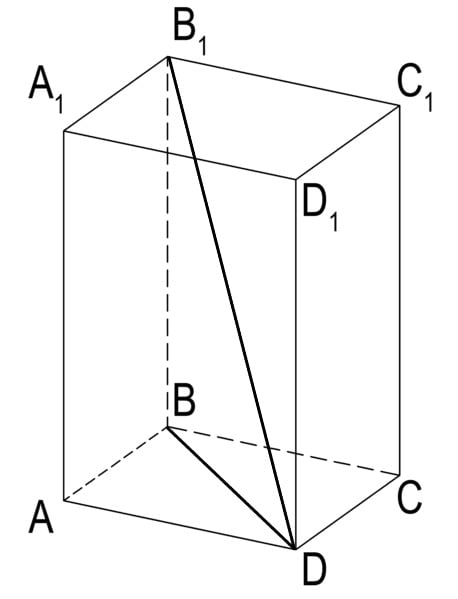
Triângulo (ABDA): d² = a² + b² (1)
Triângulo : D² = c² + d² (2)
Substituindo (2) em (1): D² = a² + b² + c²
Uma dica que pode facilitar bastante na hora de resolver, ou desenvolver, os cálculos é observando as figuras espaciais nas três vistas (frontal, lateral e superior), usando principalmente as duas últimas que não são convencionais.
Vídeos sobre prisma
Sólidos geométricos
Nesse vídeo, a Professo Flávia usa uma estratégia curiosa para ajudar o nosso cérebro a lembrar os pontos principais que compõem os prismas. Em seguida ela nos dá a relação de número de vértices, faces e arestas de cada uma das formas geométricas expostas. Vale a pena conferir!
Prismas: conceitos iniciais – definição e classificação
O conteúdo ministrado pelo Professor Paulo esmiuça e revisa alguns conceitos que aprendemos sobre os prismas ao longo do nosso texto, desde conceitos básicos à diferenciação de um prisma reto, oblíquo e regular. Aproveite para tirar suas dúvidas.
Geometria espacial – Exercícios de Prismas 1 e 2
Hora de colocar a mão na massa! O Professor Leandro já vai direto na abordagem prática da geometria espacial, este vídeo trás o desenvolvimento dos cálculos de prismas. Então esse vídeo pode te ajudar a tornar mais evidente e facilitar a aplicação das fórmulas que aprendemos anteriormente.
Compartilhe esse artigo










